The main role of the competition ladder is to provide a summary of the past. In this blog we'll be assessing what they can tell us about the future. Specifically, we'll be looking at what can be inferred about the make up of the finals by reviewing the competition ladder at different points of the season.
I'll be restricting my analysis to the seasons 1997-2009 (which sounds a bit like a special category for Einstein Factor, I know) as these seasons all had a final 8, twenty-two rounds and were contested by the same 16 teams - not that this last feature is particularly important.
Let's start by asking the question: for each season and on average how many of the teams in the top 8 at a given point in the season go on to play in the finals?
The first row of the table shows how many of the teams that were in the top 8 after the 1st round - that is, of the teams that won their first match of the season - went on to play in September. A chance result would be 4, and in 7 of the 13 seasons the actual number was higher than this. On average, just under 4.5 of the teams that were in the top 8 after 1 round went on to play in the finals.
This average number of teams from the current Top 8 making the final Top 8 grows steadily as we move through the rounds of the first half of the season, crossing 5 after Round 2, and 6 after Round 7. In other words, historically, three-quarters of the finalists have been determined after less than one-third of the season. The 7th team to play in the finals is generally not determined until Round 15, and even after 20 rounds there have still been changes in the finalists in 5 of the 13 seasons.
Last year is notable for the fact that the composition of the final 8 was revealed - not that we knew - at the end of Round 12 and this roster of teams changed only briefly, for Rounds 18 and 19, before solidifying for the rest of the season.
Next we ask a different question: if your team's in ladder position X after Y rounds where, on average, can you expect it to finish.
Regression to the mean is on abundant display in this table with teams in higher ladder positions tending to fall and those in lower positions tending to rise. That aside, one of the interesting features about this table for me is the extent to which teams in 1st at any given point do so much better than teams in 2nd at the same point. After Round 4, for example, the difference is 2.6 ladder positions.
Another phenomenon that caught my eye was the tendency for teams in 8th position to climb the ladder while those in 9th tend to fall, contrary to the overall tendency for regression to the mean already noted.
One final feature that I'll point out is what I'll call the Discouragement Effect (but might, more cynically and possibly accurately, have called it the Priority Pick Effect), which seems to afflict teams that are in last place after Round 5. On average, these teams climb only 2 places during the remainder of the season.
Averages, of course, can be misleading, so rather than looking at the average finishing ladder position, let's look at the proportion of times that a team in ladder position X after Y rounds goes on to make the final 8.
One immediately striking result from this table is the fact that the team that led the competition after 1 round - which will be the team that won with the largest ratio of points for to points against - went on to make the finals in 12 of the 13 seasons.
You can use this table to determine when a team is a lock or is no chance to make the final 8. For example, no team has made the final 8 from last place at the end of Round 5. Also, two teams as lowly ranked as 12th after 13 rounds have gone on to play in the finals, and one team that was ranked 12th after 17 rounds still made the September cut.
If your team is in 1st or 2nd place after 10 rounds you have history on your side for them making the top 8 and if they're higher than 4th after 16 rounds you can sport a similarly warm inner glow.
Lastly, if your aspirations for your team are for a top 4 finish here's the same table but with the percentages in terms of making the Top 4 not the Top 8.
Perhaps the most interesting fact to extract from this table is how unstable the Top 4 is. For example, even as late as the end of Round 21 only 62% of the teams in 4th spot have finished in the Top 4. In 2 of the 13 seasons a Top 4 spot has been grabbed by a team in 6th or 7th at the end of the penultimate round.
It had been rankling me that I'd not come up with a way to validate any of the LAMP, HAMP or HELP models that I chronicled the development of in earlier blogs.
In retrospect, what I probably should have done is build the models using only the data for seasons 2006 to 2008 and then test the resulting models on 2009 data but you can't unscramble an egg and, statistically speaking, my hen's albumen and vitellus are well and truly curdled.
Then I realised that there is though another way to test the models - well, for now at least, to test the HELP model.
Any testing needs to address the major criticism that could be levelled at the HELP model, which is a criticism stemming from its provenance. The final HELP model is the one that, amongst the many thousands of HELP-like models that my computer script briefly considered (and, as we'll see later, of the thousands of billions that it might have considered), was able to be made to best fit the line betting data for 2008 and 2009, projecting one round into the future using any or all of 47 floating window models available to it.
From an evolutionary viewpoint the HELP model represents an organism astonishingly well-adapted to the environment in which its genetic blueprint was forged, but whether HELP will be the dinosaur or the horseshoe crab equivalent in the football modelling universe is very much an open question.
With the possible criticism I've just described in mind, what I've done to test the HELP model is to estimate the fit that could be achieved with the modelling technique used to find HELP had the line betting result history been different but similar. Specifically,what I've done is taken the actual timeseries of line betting results, randomised them, run the same script that I used to create HELP and then calculated how well the best model the script can find fits the alternative timeseries of line betting outcomes.
Let me explain what I mean by randomising the timeseries of line betting results by using a shortened example. If, say, the real, original timeseries of line betting results were (Home Team Wins, Home Team Loses, Home Team Loses, Home Team Wins, Home Team Wins) then, for one of my simulations, I might have used the sequence (Home Team Wins, Home Team Wins, Home Team Wins, Home Team Loses, Home Team Loses), which is the same set of results but in a different order.
From a statistical point of view, it's important that the randomised sequences used have the same proportions of "Home Team Wins" and "Home Team Loses" as the original, real series, because part of the predictive power of the HELP model might come from its exploiting the imbalance between these two proportions. To give a simple example, if I fitted a model to the roll of a die and its job was to predict "Roll is a 6" or "Roll is not a 6", a model that predicted "Roll is not a 6" every time would achieve an 83% hit rate solely from picking up on the imbalance in the data to be modelled. The next thing you know, someone introduces a Dungeons & Dragons 20-sided dice and your previously impressive Die Prediction Engine self-immolates before your eyes.
Having created the new line betting results history in the manner described above, the simulation script proceeds by creating the set of floating window models - that is, the models that look only at the most recent X rounds of line betting and home team bookie price data for X ranging from 6 to 52 - then selects a subset of these models and determines the week-to-week weighting of these models that best fits the most recent 26 rounds of data. This optimal linear combination of floating window models is then used to predict the results for the following round. You might recall that this is exactly the method used to create the HELP model in the first place.
The model that is built using the currently best-fitting linear combination of floating window models is, after a fixed number of models have been considered, declared the winner and the percentage of games that it correctly predicts is recorded. The search then recommences with a different set of line betting outcomes, again generated using the method described earlier and another, new winning model is found for this line betting history and its performance noted.
In essence, the models constructed in this way tell us to what extent the technique I used to create HELP can be made to fit a number of arbitrary sequences of line betting results, each of which has the same proportion of Home Team wins and losses as the original, real sequence. The better the average fit that I can achieve to such an arbitrary sequence, the less confidence I can have that the HELP model has actually modelled something inherent in the real line betting results for seasons 2008 and 2009 and the more I should be concerned that all I've got is a chameleonic modelling technique capable of creating a model flexible enough to match any arbitrary set of results - which would be a bad thing.
You'll recall that there are 47 floating window models that can be included in the final model, one floating window model that uses only the past 6 weeks, another that uses the past 7 weeks, and so on up to one that uses the past 52 weeks. If you do the combinatorial maths you'll discover that there are almost 141,000 billion different models that can be constructed using one or more of the floating window models.
The script I've written evaluates one candidate model about every 1.5 seconds so it would take about 6.7 billion years for it to evaluate them all. That would allow us to get a few runs in before the touted heat death of the universe, but it is at the upper end of most people's tolerance for waiting. Now, undoubtedly, my code could do with some optimisation, but unless I can find a way to make it run about 13 billion times faster it'll be quicker to revert to the original idea of letting the current season serve as the test of HELP rather than use the test protocol I've proposed here. Consequently I'm forced to accept that any conclusions I come to about whether of not the performance of the HELP model's is all down to chance are of necessity only indicative.
That said there is one statistical modelling 'trick' I can use to improve the potential for my script to find "good" models and that is to bias the combinations of floating window models that my script considers towards those combinations that are similar to those that have already demonstrated above-average performance during the simulation so far. So, for example, if a model using the 7-round, 9-round and 12-round floating window models look promising, the script might next look at a model using the 7-round, 9-round and 40-round floating window models (ie change just one of the underlying models) or it might look at a model using the 7-round, 9-round, 12-round and 45-round floating window models (ie add another floating model). This is a very rudimentary version of what the trade calls a Genetic Algorithm and it is exactly the same approach I used in finding the final HELP model.
You might recall that HELP achieved an accuracy of 60.8% across seasons 2008 and 2009, so the statistic that I've had the script track is how often the winning model created for a given set of line betting outcomes performs as well as or better than the HELP model.
From the testing I've done so far my best estimate of the likelihood that the HELP model's performance can be adequately explained by chance alone is between 5 and 35%. That's maddeningly wide and spans the interval from "statistically significant" to "wholly unconvincing" so I'll continue to run tests over the next few weeks as I'm able to tie up my computer doing so.
How would you characterise the Grand Finals that you've witnessed? As low-scoring, closely fought games; as high-scoring games with regular blow-out finishes; or as something else?
First let's look at the total points scored in Grand Finals relative to the average points scored per game in the season that immediately preceded them.
Apart from a period spanning about the first 25 years of the competition, during which Grand Finals tended to be lower-scoring affairs than the matches that took place leading up to them, Grand Finals have been about as likely to produce more points than the season average as to produce fewer points.
One way to demonstrate this is to group and summarise the Grand Finals and non-Grand Finals by the decade in which they occurred.
There's no real justification then, it seems, in characterising them as dour affairs.
That said, there have been a number of Grand Finals that failed to produce more than 150 points between the two sides - 49 overall, but only 3 of the last 30. The most recent of these was the 2005 Grand Final in which Sydney's 8.10 (58) was just good enough to trump the Eagles' 7.12 (54). Low-scoring, sure, but the sort of game for which the cliche "modern-day classic" was coined.
To find the lowest-scoring Grand Final of all time you'd need to wander back to 1927 when Collingwood 2.13 (25) out-yawned Richmond 1.7 (13). Collingwood, with efficiency in mind, got all of its goal-scoring out of the way by the main break, kicking 2.6 (20) in the first half. Richmond, instead, left something in the tank, going into the main break at 0.4 (4) before unleashing a devastating but ultimately unsuccessful 1.3 (9) scoring flurry in the second half.
That's 23 scoring shots combined, only 3 of them goals, comprising 12 scoring shots in the first half and 11 in the second. You could see that many in an under 10s soccer game most weekends.
Forty-five years later, in 1972, Carlton and Richmond produced the highest-scoring Grand Final so far. In that game, Carlton 28.9 (177) held off a fast-finishing Richmond 22.18 (150), with Richmond kicking 7.3 (45) to Carlton's 3.0 (18) in the final term.
Just a few weeks earlier these same teams had played out an 8.13 (63) to 8.13 (63) draw in their Semi Final. In the replay Richmond prevailed 15.20 (110) to Carlton's 9.15 (69) meaning that, combined, the two Semi Finals they played generated 22 points fewer than did the Grand Final.
From total points we turn to victory margins.
Here too, again save for a period spanning about the first 35 years of the competition during which GFs tended to be closer fought than the average games that had gone before them, Grand Finals have been about as likely to be won by a margin smaller than the season average as to be won by a greater margin.
Of the 10 most recent Grand Finals, 5 have produced margins smaller than the season average and 5 have produced greater margins.
Perhaps a better view of the history of Grand Final margins is produced by looking at the actual margins rather than the margins relative to the season average. This next table looks at the actual margins of victory in Grand Finals summarised by decade.
One feature of this table is the scarcity of close finishes in Grand Finals of the 1980s, 1990s and 2000s. Only 4 of these Grand Finals have produced a victory margin of less than 3 goals. In fact, 19 of the 29 Grand Finals have been won by 5 goals or more.
An interesting way to put this period of generally one-sided Grand Finals into historical perspective is provided by this, the final graphic for today.
They just don't make close Grand Finals like they used to.
If you were to consider each quarter of football as a separate contest, what pattern of wins and losses do you think has been most common? Would it be where one team wins all 4 quarters and the other therefore losses all 4? Instead, might it be where teams alternated, winning one and losing the next, or vice versa? Or would it be something else entirely?
The answer, it turns out, depends on the period of history over which you ask the question. Here's the data:
So, if you consider the entire expanse of VFL/AFL history, the egalitarian "WLWL / LWLW" cadence has been most common, occurring in over 18% of all games. The next most common cadence, coming in at just under 15% is "WWWW / LLLL" - the Clean Sweep, if you will. The next four most common cadences all have one team winning 3 quarters and the other winning the remaining quarter, each of which such cadences have occurred about 10-12% of the time. The other patterns have occurred with frequencies as shown under the 1897 to 2009 columns, and taper off to the rarest of all combinations in which 3 quarters were drawn and the other - the third quarter as it happens - was won by one team and so lost by the other. This game took place in Round 13 of 1901 and involved Fitzroy and Collingwood.
If, instead, you were only to consider more recent seasons excluding the current one, say from 1980 to 2008, you'd find that the most common cadence has been the Clean Sweep on about 18%, with the "WLLL / "LWWW" cadence in second on a little over 12%. Four other cadences then follow in the 10-11.5% range, three of them involving one team winning 3 of the 4 quarters and the other the "WLWL / LWLW" cadence.
In short it seems that teams have tended to dominate contests more in the 1980 to 2008 period than had been the case historically.
(It's interesting to note that, amongst those games where the quarters are split 2 each, "WLWL / LWLW" is more common than either of the two other possible cadences, especially across the entire history of footy.)
Turning next to the current season, we find that the Clean Sweep has been the most common cadence, but is only a little ahead of 5 other cadences, 3 of these involving a 3-1 split of quarters and 2 of them involving a 2-2 split.
So, 2009 looks more like the period 1980 to 2008 than it does the period 1897 to 2009.
What about the evidence for within-game momentum in the quarter-to-quarter cadence? In other words, are teams who've won the previous quarter more or less likely to win the next?
Once again, the answer depends on your timeframe.
Across the period 1897 to 2009 (and ignoring games where one of the two relevant quarters was drawn):
So, across the entire history of football, there's been, if anything, an anti-momentum effect, since teams that win one quarter have been a little less likely to win the next.
Inspecting the record for more recent times, however, consistent with our earlier conclusion about the greater tendency for teams to dominate matches, we find that, for the periods 1980 to 2008 (and, in brackets, for 2009):
In more recent history then, there is evidence of within-game momentum.
All of which would lead you to believe that winning the 1st quarter should be particularly important, since it gets the momentum moving in the right direction right from the start. And, indeed, this season that has been the case, as teams that have won matches have also won the 1st quarter in 71% of those games, the greatest proportion of any quarter.
You've wagered on Geelong - a line bet in which you've given 46.5 points start - and they lead by 42 points at three-quarter time. What price should you accept from someone wanting to purchase your wager? They also led by 44 points at quarter time and 43 points at half time. What prices should you have accepted then?
In this blog I've analysed line betting results since 2006 and derived three models to answer questions similar the one above. These models take as inputs the handicap offered by the favourite and the favourite's margin relative to that handicap at a particular quarter break. The output they provide is the probability that the favourite will go on to cover the spread given the situation they find themselves in at the end of some quarter.
The chart below plots these probabilities against margins relative to the spread at quarter time for 8 different handicap levels.
Negative margins mean that the favourite has already covered the spread, positive margins that there's still some spread to be covered.
The top line tracks the probability that a 47.5 point favourite covers the spread given different margins relative to the spread at quarter time. So, for example, if the favourite has the spread covered by 5.5 points (ie leads by 53 points) at quarter time, there's a 90% chance that the favourite will go on to cover the spread at full time.
In comparison, the bottom line tracks the probability that a 6.5 point favourite covers the spread given different margins relative to the spread at quarter time. If a favourite such as this has the spread covered by 5.5 points (ie leads by 12 points) at quarter time, there's only a 60% chance that this team will go on to cover the spread at full time. The logic of this is that a 6.5 point favourite is, relatively, less strong than a 47.5 point favourite and so more liable to fail to cover the spread for any given margin relative to the spread at quarter time.
Another way to look at this same data is to create a table showing what margin relative to the spread is required for an X-point favourite to have a given probability of covering the spread.
So, for example, for the chances of covering the spread to be even, a 6.5 point favourite can afford to lead by only 4 or 5 (ie be 2 points short of covering) at quarter time and a 47.5 point favourite can afford to lead by only 8 or 9 (ie be 39 points short of covering).
The following diagrams provide the same chart and table for the favourite's position at half time.
Finally, these next diagrams provide the same chart and table for the favourite's position at three-quarter time.
I find this last table especially interesting as it shows how fine the difference is at three-quarter time between likely success and possible failure in terms of covering the spread. The difference between a 50% and a 75% probability of covering is only about 9 points and between a 75% and a 90% probability is only 9 points more.
To finish then, let's go back to the question with which I started this blog. A 46.5 point favourite leading by 42 points at three-quarter time is about a 69.4% chance to go on and cover. So, assuming you backed the favourite at $1.90 your expected payout for a 1 unit wager is 0.694 x 0.9 - 0.306 = +0.32 units. So, you'd want to be paid 1.32 units for your wager, given that you also want your original stake back too.
A 46.5 point favourite leading by 44 points at quarter time is about an 85.5% chance to go on and cover, and a similar favourite leading by 43 points at half time is about an 84.7% chance to go on to cover. The expected payouts for these are +0.62 and +0.61 units respectively, so you'd have wanted about 1.62 units to surrender these bets (a little more if you're a risk-taker and a little less if you're risk-averse, but that's a topic for another day ...)
In a famous - some might say, infamous - paper by Wolfers he analysed the results of 44,120 NCAA Division I basketball games on which public betting was possible, looking for signs of "point shaving".
Point shaving occurs when a favoured team plays well enough to win, but deliberately not quite well enough to cover the spread. In his first paragraph he states: "Initial evidence suggests that point shaving may be quite widespread". Unsurprisingly, such a conclusion created considerable alarm and led, amongst a slew of furious rebuttals, to a paper by sabermetrician Phil Birnbaum refuting Wolfers' claim. This, in turn, led to a counter-rebuttal by Wolfers.
Wolfers' claim is based on a simple finding: in the games that he looked at, strong favourites - which he defines as those giving more than 12 points start - narrowly fail to cover the spread significantly more often than they narrowly cover the spread. The "significance" of the difference is in a statistical sense and relies on the assumption that the handicap-adjusted victory margin for favourites has a zero mean, normal distribution.
He excludes narrow favourites from his analysis on the basis that, since they give relatively little start, there's too great a risk that an attempt at point-shaving will cascade into a loss not just on handicap but outright. Point-shavers, he contends, are happy to facilitate a loss on handicap but not at the risk of missing out on the competition points altogether and of heightening the levels of suspicion about the outcome generally.
I have collected over three-and-a-half seasons of TAB Sporsbet handicapping data and results, so I thought I'd perform a Wolfers style analysis on it. From the outset I should note that one major drawback of performing this analysis on the AFL is that there are multiple line markets on AFL games and they regularly offer different points start. So, any conclusions we draw will be relevant only in the context of the starts offered by TAB Sportsbet. A "narrow shaving" if you will.
In adapting Wolfers' approach to AFL I have defined a "strong favourite" as a team giving more than 2 goals start though, from a point-shaving perspective, the conclusion is the same if we define it more restrictively. Also, I've defined "narrow victory" with respect to the handicap as one by less than 6 points. With these definitions, the key numbers in the table below are those in the box shaded grey.
These numbers tell us that there have been 27(13+4+10) games in which the favourite has given 12.5 points or more start and has won, by has won narrowly by enough to cover the spread. As well, there have been 24(11+7+6) games in which the favourite has given 12.5 points or more start and has won, but has narrowly not won by enough to cover the spread. In this admittedly small sample of just 51 games, there is then no statistical evidence at all of any point-shaving going on. In truth if there was any such behaviour occurring it would need to be near-endemic to show up in a sample this small lest it be washed out by the underlying variability.
So, no smoking gun there - not even a faint whiff of gunpowder ...
The table does, however, offer one intriguing insight, albeit that it only whispers it.
The final column contains the percentage of the time that favourites have managed to cover the spread for the given range of handicaps. So, for example, favourites giving 6.5 points start have covered the spread 53% of the time. Bear in mind that these percentages should be about 50%, give or take some statistically variability, lest they be financially exploitable.
It's the next percentage down that's the tantalising one. Favourites giving 7.5 to 11.5 points start have, over the period 2006 to Round 13 of 2009, covered the spread only 41% of the time. That percentage is statistically significantly different from 50% at roughly the 5% level (using a two-tailed test in case you were wondering). If this failure to cover continues at this rate into the future, that's a seriously exploitable discrepancy.
To check if what we've found is merely a single-year phenomenon, let's take a look at the year-by-year data. In 2006, 7.5-to 11.5-point favourites covered on only 12 of 35 occasions (34%). In 2007, they covered in 17 of 38 (45%), while in 2008 they covered in 12 of 28 (43%). This year, to date they've covered in 6 of 15 (40%). So there's a thread of consistency there. Worth keeping an eye on, I'd say.
Another striking feature of this final column is how the percentage of time that the favourites cover tends to increase with the size of the start offered and only crosses 50% for the uppermost category, suggesting perhaps a reticence on the part of TAB Sportsbet to offer appropriately large starts for very strong favourites. Note though that the discrepancy for the 24.5 points or more category is not statistically significant.
One aspect of the unusual predictability of this year's AFL results has gone - at least to my knowledge - unremarked.
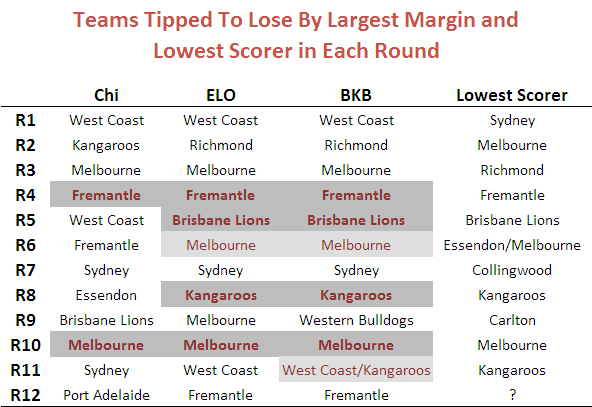
That aspect is the extent to which the week's low-scoring team has been the team receiving the most points start on Sportsbet. Following this strategy would have been successful in six of the last eight rounds, albeit that in one of those rounds there were joint low-scorers and, in another, there were two teams both receiving the most start.
The table below provides the detail and also shows the teams that Chi and ELO would have predicted as the low scorers (proxied by the team they selected to lose by the biggest margin). Correct predictions are shaded dark grey. "Half right" predictions - where there's a joint prediction, one of which is correct, or a joint low-scorer, one of which was predicted - are shaded light grey.
To put the BKB performance in context, here's the data for seasons 2006 to 2009.
All of which might appear to amount to not much until you understand that Sportsbet fields a market on the round's lowest scorer. So we should keep an eye on this phenomenon in subsequent weeks to see if the apparent lift in the predictability of the low scorer is a statistical anomaly or something more permanent and exploitable. In fact, there might still be a market opportunity even if historical rates of predictiveness prevail, provided the average payoff is high enough.
The curse of the unbalanced draw remains in the AFL this year and teams will once again finish in ladder positions that they don't deserve. As long-time MAFL readers will know, this is a topic I've returned to on a number of occasions but, in the past, I've not attempted to quantify its effects.
This week, however, a MAFL Investor sent me a copy of a paper that's been prepared by Liam Lenten of the School of Economics and Finance at La Trobe University for a Research Seminar Series to be held later this month and in which he provides a simple methodology for projecting how each team would have fared had they played the full 30-game schedule, facing every other team twice.
For once I'll spare you the details of the calculation and just provide an overview. Put simply, Lenten's method adjusts each team's actual win ratio (the proportion of games that it won across the entire season counting draws as one-half a win) based on the average win ratios of all the teams it met only once. If the teams it met only once were generally weaker teams - that is, teams with low win ratios - then its win ratio will be adjusted upwards to reflect the fact that, had these weaker teams been played a second time, the team whose ratio we're considering might reasonably have expected to win a proportion of them greater than their actual win ratio.
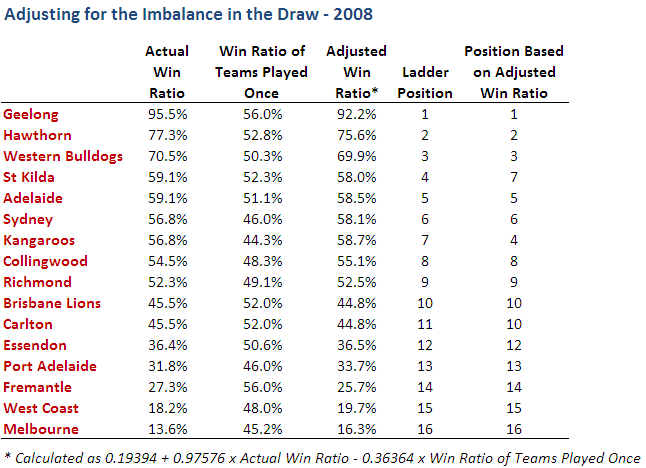
As ever, an example might help. So, here's the detail for last year.
Consider the row for Geelong. In the actual home and away season they won 21 from 22 games, which gives them a win ratio of 95.5%. The teams they played only once - Adelaide, Brisbane Lions, Carlton, Collingwood, Essendon, Hawthorn, St Kilda and the Western Bulldogs - had an average win ratio of 56.0%. Surprisingly, this is the highest average win ratio amongst teams played only once for any of the teams, which means that, in some sense, Geelong had the easiest draw of all the teams. (Although I do again point out that it benefited heavily from not facing itself at all during the season, a circumstance not enjoyed by any other team.)
The relatively high average win ratio of the teams that Geelong met only once serves to depress their adjusted win ratio, moving it to 92.2%, still comfortably the best in the league.
Once the calculations have been completed for all teams we can use the adjusted win ratios to rank them. Comparing this ranking with that of the end of season ladder we find that the ladder's 4th-placed St Kilda swap with the 7th-placed Roos and that the Lions and Carlton are now tied rather than being split by percentages as they were on the actual end of season ladder. So, the only significant difference is that the Saints lose the double chance and the Roos gain it.
If we look instead at the 2007 season, we find that the Lenten method produces much greater change.
In this case, eight teams' positions change - nine if we count Fremantle's tie with the Lions under the Lenten method. Within the top eight, Port Adelaide and West Coast swap 2nd and 3rd, and Collingwood and Adelaide swap 6th and 8th. In the bottom half of the ladder, Essendon and the Bulldogs swap 12th and 13th, and, perhaps most important of all, the Tigers lose the Spoon and the priority draft pick to the Blues.
In Lenten's paper he looks at the previous 12 seasons and finds that, on average, five to six teams change positions each season. Furthermore, he finds that the temporal biases in the draw have led to particular teams being regularly favoured and others being regularly handicapped. The teams that have, on average, suffered at the hands of the draw have been (in order of most affected to least) Adelaide, West Coast, Richmond, Fremantle, Western Bulldogs, Port Adelaide, Brisbane Lions, Kangaroos, Carlton. The size of these injustices range from an average 1.11% adjustment required to turn Adelaide's actual win ratio into an adjusted win ratio, to just 0.03% for Carlton.
On the other hand, teams that have benefited, on average, from the draw have been (in order of most benefited to least) Hawthorn, St Kilda, Essendon, Geelong, Collingwood, Sydney and Melbourne. Here the average benefits range from 0.94% for Hawthorn to 0.18% for Melbourne.
I don't think that the Lenten work is the last word on the topic of "unbalance", but it does provide a simple and reasonably equitable way of quantitatively dealing with its effects. It does not, however, account for any inter-seasonal variability in team strengths nor, more importantly, for the existence any home ground advantage.
Still, if it adds one more finger to the scales on the side of promoting two full home and away rounds, it can't be a bad thing can it?
Last year, 20 games in the home and away season were decided by less than a goal and two teams, Richmond and Sydney were each involved in 5 of them.
Relatively speaking, the Tigers and the Swans fared quite well in these close finishes, each winning three, drawing one and losing just one of the five contests.
Fremantle, on the other hand, had a particularly bad run in close games last years, losing all four of those it played in, which contributed to an altogether forgettable year for the Dockers.
The table below shows each team's record in close games across the previous five seasons.
Surprisingly, perhaps, the Saints head the table with a 71% success rate in close finishes across the period 2004-2008. They've done no worse than 50% in close finishes in any of the previous five seasons, during which they've made three finals appearances.
Next best is West Coast on 69%, a figure that would have been higher but for an 0 and 1 performance last year, which was also the only season in the previous five during which they missed the finals.
Richmond have the next best record, despite missing the finals in all five seasons. They're also the team that has participated in the greatest number of close finishes, racking up 16 in all, one ahead of Sydney, and two ahead of Port.
The foot of the table is occupied by Adelaide, whose 3 and 9 record includes no season with a better than 50% performance. Nonetheless they've made the finals in four of the five years.
Above Adelaide are the Hawks with a 3 and 6 record, though they are 3 and 1 for seasons 2006-2008, which also happen to be the three seasons in which they've made the finals.
So, from what we've seen already, there seems to be some relationship between winning the close games and participating in September's festivities. The last two rows of the table shed some light on this issue and show us that Finalists have a 58% record in close finishes whereas Non-Finalists have only a 41% record.
At first, that 58% figure seems a little low. After all, we know that the teams we're considering are Finalists, so they should as a group win well over 50% of their matches. Indeed, over the five year period they won about 65% of their matches. It seems then that Finalists fare relatively badly in close games compared to their overall record.
However, some of those close finishes must be between teams that both finished in the finals, and the percentage for these games is by necessity 50% (since there's a winner and a loser in each game, or two teams with draws). In fact, of the 69 close finishes in which Finalists appeared, 29 of them were Finalist v Finalist matchups.
When we look instead at those close finishes that pitted a Finalist against a Non-Finalist we find that there were 40 such clashes and that the Finalist prevailed in about 70% of them.
So that all seems as it should be.
Today we'll revisit yet another chestnut and we'll analyse a completely new statistic.
First, the chestnut: which quarter do winning teams win most often? You might recall that for the previous four seasons the answer has been the 3rd quarter, although it was a very close run thing last season, when the results for the 3rd and 4th quarters were nearly identical.
How then does the picture look if we go back across the entire history of the VFL/AFL?
It turns out that the most recent epoch, spanning the seasons 1993 to 2008, has been one in which winning teams have tended to win more 3rd quarters than any other quarter. In fact, it was the quarter won most often in nine of those 16 seasons.
This, however, has not at all been the norm. In four of the other six epochs it has been the 4th quarter that winning teams have tended to win most often. In the other three epochs the 4th quarter has been the second most commonly won quarter.
But, the 3rd quarter has rarely been far behind the 4th, and its resurgence in the most recent epoch has left it narrowly in second place in the all-time statistics.
A couple of other points are worth making about the table above. Firstly, it's interesting to note how significantly more frequently winning teams are winning the 1st quarter than they have tended to in epochs past. Successful teams nowadays must perform from the first bounce.
Secondly, there's a clear trend over the past 4 epochs for winning teams to win a larger proportion of all quarters, from about 66% in the 1945 to 1960 epoch to almost 71% in the 1993 to 2008 epoch.
Now on to something a little different. While I was conducted the previous analysis, I got to wondering if there'd ever been a team that had won a match in which in had scored more points than its opponent in just a solitary quarter. Incredibly, I found that it's a far more common occurrence than I'd have estimated.
The red line shows, for every season, the percentage of games in which the winner won just a solitary quarter (they might or might not have drawn any of the others). The average percentage across all 112 seasons is 3.8%. There were five such games last season, in four of which the winner didn't even manage to draw any of the other three quarters. One of these games was the Round 19 clash between Sydney and Fremantle in which Sydney lost the 1st, 2nd and 4th quarters but still got home by 2 points on the strength of a 6.2 to 2.5 3rd term.
You can also see from the chart the upward trend since about the mid 1930s in the percentage of games in which the winner wins all four quarters, which is consistent with the general rise, albeit much less steadily, in average victory margins over that same period that we saw in an earlier blog.
To finish, here's the same data from the chart above summarised by epoch:
MAFL is a website for ...
Click on the envelope
Copyright © 2006-2023, Tony Corke. All rights reserved.
