Previously, on at least a few occasions, I've looked at the topic of the Favourite-Longshot Bias and whether or not it exists in the TAB Sportsbet wagering markets for AFL.
A Favourite-Longshot Bias (FLB) is said to exist when favourites win at a rate in excess of their price-implied probability and longshots win at a rate less than their price-implied probability. So if, for example, teams priced at $10 - ignoring the vig for now - win at a rate of just 1 time in 15, this would be evidence for a bias against longshots. In addition, if teams priced at $1.10 won, say, 99% of the time, this would be evidence for a bias towards favourites.
When I've considered this topic in the past I've generally produced tables such as the following, which are highly suggestive of the existence of such an FLB.
Each row of this table, which is based on all games from 2006 to the present, corresponds to the results for teams with price-implied probabilities in a given range. The first row, for example, is for all those teams whose price-implied probability was less than 10%. This equates, roughly, to teams priced at $9.50 or more. The average implied probability for these teams has been 9%, yet they've won at a rate of only 4%, less than one-half of their 'expected' rate of victory.
As you move down the table you need to arrive at the second-last row before you come to one where the win rate exceed the expected rate (ie the average implied probability). That's fairly compelling evidence for an FLB.
This empirical analysis is interesting as far as it goes, but we need a more rigorous statistical approach if we're to take it much further. And heck, one of the things I do for a living is build statistical models, so you'd think that by now I might have thrown such a model at the topic ...
A bit of poking around on the net uncovered this paper which proposes an eminently suitable modelling approach, using what are called conditional logit models.
In this formulation we seek to explain a team's winning rate purely as a function of (the natural log of) its price-implied probability. There's only one parameter to fit in such a model and its value tells us whether or not there's evidence for an FLB: if it's greater than 1 then there is evidence for an FLB, and the larger it is the more pronounced is the bias.
When we fit this model to the data for the period 2006 to 2010 the fitted value of the parameter is 1.06, which provides evidence for a moderate level of FLB. The following table gives you some idea of the size and nature of the bias.
The first row applies to those teams whose price-implied probability of victory is 10%. A fair-value price for such teams would be $10 but, with a 6% vig applied, these teams would carry a market price of around $9.40. The modelled win rate for these teams is just 9%, which is slightly less than their implied probability. So, even if you were able to bet on these teams at their fair-value price of $10, you'd lose money in the long run. Because, instead, you can only bet on them at $9.40 or thereabouts, in reality you lose even more - about 16c in the dollar, as the last column shows.
We need to move all the way down to the row for teams with 60% implied probabilities before we reach a row where the modelled win rate exceeds the implied probability. The excess is not, regrettably, enough to overcome the vig, which is why the rightmost entry for this row is also negative - as, indeed, it is for every other row underneath the 60% row.
Conclusion: there has been an FLB on the TAB Sportsbet market for AFL across the period 2006-2010, but it hasn't been generally exploitable (at least to level-stake wagering).
The modelling approach I've adopted also allows us to consider subsets of the data to see if there's any evidence for an FLB in those subsets.
I've looked firstly at the evidence for FLB considering just one season at a time, then considering only particular rounds across the five seasons.
So, there is evidence for an FLB for every season except 2007. For that season there's evidence of a reverse FLB, which means that longshots won more often than they were expected to and favourites won less often. In fact, in that season, the modelled success rate of teams with implied probabilities of 20% or less was sufficiently high to overcome the vig and make wagering on them a profitable strategy.
That year aside, 2010 has been the year with the smallest FLB. One way to interpret this is as evidence for an increasing level of sophistication in the TAB Sportsbet wagering market, from punters or the bookie, or both. Let's hope not.
Turning next to a consideration of portions of the season, we can see that there's tended to be a very mild reverse FLB through rounds 1 to 6, a mild to strong FLB across rounds 7 to 16, a mild reverse FLB for the last 6 rounds of the season and a huge FLB in the finals. There's a reminder in that for all punters: longshots rarely win finals.
Lastly, I considered a few more subsets, and found:
FLB: done.
Okay, this is probably going to be a long blog so you might want to make yourself comfortable.
For some time now I've been wondering about the statistical properties of the Handicap-Adjusted Margin (HAM). Does it, for example, follow a normal distribution with zero mean?
Well firstly we need to deal with the definition of the term HAM, for which there is - at least - two logical definitions.
The first definition, which is the one I usually use, is calculated from the Home Team perspective and is Home Team Score - Away Team Score + Home Team's Handicap (where the Handicap is negative if the Home Team is giving start and positive otherwise). Let's call this Home HAM.
As an example, if the Home Team wins 112 to 80 and was giving 20.5 points start, then Home HAM is 112-80-20.5 = +11.5 points, meaning that the Home Team won by 11.5 points on handicap.
The other approach defines HAM in terms of the Favourite Team and is Favourite Team Score - Underdog Team Score + Favourite Team's Handicap (where the Handicap is always negative as, by definition the Favourite Team is giving start). Let's call this Favourite HAM.
So, if the Favourite Team wins 82 to 75 and was giving 15.5 points start, then Favourite HAM is 82-75-15.5 = -7.5 points, meaning that the Favourite Team lost by 7.5 points on handicap.
Home HAM will be the same as Favourite HAM if the Home Team is Favourite. Otherwise Home HAM and Favourite HAM will have opposite signs.
There is one other definitional detail we need to deal with and that is which handicap to use. Each week a number of betting shops publish line markets and they often differ in the starts and the prices offered for each team. For this blog I'm going to use TAB Sportsbet's handicap markets.
TAB Sportsbet Handicap markets work by offering even money odds (less the vigorish) on both teams, with one team receiving start and the other offering that same start. The only exception to this is when the teams are fairly evenly matched in which case the start is fixed at 6.5 points and the prices varied away from even money as required. So, for example, we might see Essendon +6.5 points against Carlton but priced at $1.70 reflecting the fact that 6.5 points makes Essendon in the bookie's opinion more likely to win on handicap than to lose. Games such as this are problematic for the current analysis because the 'true' handicap is not 6.5 points but is instead something less than 6.5 points. Including these games would bias the analysis - and adjusting the start is too complex - so we'll exclude them.
So, the question now becomes is HAM Home, defined as above and using the TAB Sportsbet handicap and excluding games with 6.5 points start or fewer, normally distributed with zero mean? Similarly, is HAM Favourite so distributed?
We should expect HAM Home and HAM Favourite to have zero means because, if they don't it suggests that the Sportsbet bookie has a bias towards or against Home teams of Favourites. And, as we know, in gambling, bias is often financially exploitable.
There's no particular reason to believe that HAM Home and HAM Favourite should follow a normal distribution, however, apart from the startling ubiquity of that distribution across a range of phenomena.
Consider first the issue of zero means.
The following table provides information about Home HAMs for seasons 2006 to 2008 combined, for season 2009, and for seasons 2006 to 2009. I've isolated this season because, as we'll see, it's been a slightly unusual season for handicap betting.
Each row of this table aggregates the results for different ranges of Home Team handicaps. The first row looks at those games where the Home Team was offering start of 30.5 points or more. In these games, of which there were 53 across seasons 2006 to 2008, the average Home HAM was 1.1 and the standard deviation of the Home HAMs was 39.7. In season 2009 there have been 17 such games for which the average Home HAM has been 14.7 and the standard deviation of the Home HAMs has been 29.1.
The asterisk next to the 14.7 average denotes that this average is statistically significantly different from zero at the 10% level (using a two-tailed test). Looking at other rows you'll see there are a handful more asterisks, most notably two against the 12.5 to 17.5 points row for season 2009 denoting that the average Home HAM of 32.0 is significant at the 5% level (though it is based on only 8 games).
At the foot of the table you can see that the overall average Home HAM across seasons 2006 to 2008 was, as we expected approximately zero. Casting an eye down the column of standard deviations for these same seasons suggests that these are broadly independent of the Home Team handicap, though there is some weak evidence that larger absolute starts are associated with slightly larger standard deviations.
For season 2009, the story's a little different. The overall average is +8.4 points which, the asterisks tell us, is statistically significantly different from zero at the 5% level. The standard deviations are much smaller and, if anything, larger absolute margins seem to be associated with smaller standard deviations.
Combining all the seasons, the aberrations of 2009 are mostly washed out and we find an average Home HAM of just +1.6 points.
Next, consider Favourite HAMs, the data for which appears below:
The first thing to note about this table is the fact that none of the Favourite HAMs are significantly different from zero.
Overall, across seasons 2006 to 2008 the average Favourite HAM is just 0.1 point; in 2009 it's just -3.7 points.
In general there appears to be no systematic relationship between the start given by favourites and the standard deviation of the resulting Favourite HAMs.
Summarising:
Okay then, are Home HAMs and Favourite HAMs normally distributed?
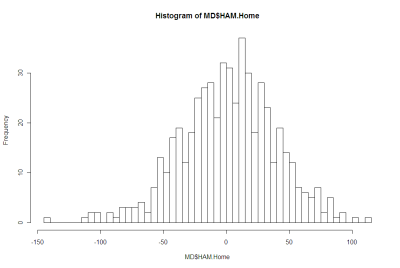
Here's a histogram of Home HAMs:
And here's a histogram of Favourite HAMs:
There's nothing in either of those that argues strongly for the negative.
More formally, Shapiro-Wilks tests fail to reject the null hypothesis that both distributions are Normal.
Using this fact, I've drawn up a couple of tables that compare the observed frequency of various results with what we'd expect if the generating distributions were Normal.
Here's the one for Home HAMs:
There is a slight over-prediction of negative Home HAMs and a corresponding under-prediction of positive Home HAMs but, overall, the fit is good and the appropriate Chi-Squared test of Goodness of Fit is passed.
And, lastly, here's the one for Home Favourites:
In this case the fit is even better.
We conclude then that it seems reasonable to treat Home HAMs as being normally distributed with zero mean and a standard deviation of 37.7 points and to treat Favourite HAMs as being normally distributed with zero mean and, curiously, the same standard deviation. I should point out for any lurking pedant that I realise neither Home HAMs nor Favourite HAMs can strictly follow a normal distribution since Home HAMs and Favourite HAMs take on only discrete values. The issue really is: practically, how good is the approximation?
This conclusion of normality has important implications for detecting possible imbalances between the line and head-to-head markets for the same game. But, for now, enough.
The other night I was chatting with a few MAFL Investors and the topic of the Favourite-Longshot bias - and whether or not it exists in TAB AFL betting - came up. Such a bias is said to exist if punters tend to do better wagering on favourites than they do wagering on longshots.
The bias has been found in a number of wagering markets, among them Major League Baseball, horse racing in the US and the UK, and even greyhound racing. In its most extreme form, so mispriced do favourites tend to be that punters can actually make money over the long haul by wagering on them. I suspect that what prevents most punters from exploiting this situation - if they're aware of it - is the glacial rate at which profits accrue unless large amounts are wagered. Wagering $1,000 on a contest with the prospect of losing it all in the event of an upset or, instead, of winning just $100 if the contest finishes as expected seems, for most punters, like a lousy way to spend a Sunday afternoon.
Anyway, I thought I'd analyse the data that I've collected over the previous 3 seasons to see if I can find any evidence of the bias. The analysis is summarised in the table below.
Clearly such a bias does exist based on my data and on my analysis, in which I've treated teams priced at $1.90 or less as favourites and those priced at $5.01 or more as longshots. Regrettably, the bias is not so pronounced that level-stake wagering on favourites becomes profitable, but it is sufficient to make such wagering far less unprofitable than wagering on longshots.
In fact, wagering on favourites - and narrow underdogs too - would be profitable but for the bookie's margin that's built into team prices, which we can see has averaged 7.65% across the last three seasons. Adjusting for that, assuming that the 7.65% margin is applied to favourites and underdogs in equal measure, wagering on teams priced under $2.50 would produce a profit of around 1-1.5%.
In the table above I've had to make some fairly arbitrary decisions about the price ranges to use, which inevitably smooths out some of the bumps that exist in the returns for certain, narrower price ranges. For example, level-stake wagering on teams priced in the range $3.41 to $3.75 would have been profitable over the last three years. Had you the prescience to follow this strategy you'd have made 32 bets and netted a profit of 9 units, which is just over 28%.
A more active though less profitable strategy would have been to level-stake wager on all teams priced in the $2.41 to $3.20 price range, which would have led you to make 148 wagers and pocket a 3.2 unit or 2.2% profit.
Alternatively, had you hired a less well-credentialled clairvoyant and as a consequence instead level-stake wagered on all the teams priced in the $1.81 to $2.30 range - a strategy that suffers in part from requiring you to bet on both teams in some games and so guarantee a loss - you'd have made 222 bets and lost 29.6 units, which is a little over a 13% loss.
Regardless, if there is a Favourite-Longshot bias, what does it mean for MAFL?
In practical terms all it means is that a strategy of wagering on every longshot would be painfully unprofitable, as last year's Heritage Fund Investors can attest. That’s not to say that there's never value in underdog wagering, just that there isn’t consistent value in doing so. What MAFL aims to do is detect and exploit any value – whether it resides in favourites or in longshots.
What MAFL also seeks to do is match the size of its bet to the magnitude of its assessed advantage. That, though, is a topic for another day.
MAFL is a website for ...
Click on the envelope
Copyright © 2006-2023, Tony Corke. All rights reserved.
